21.(本小题满分13分)
如图7,椭圆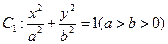 的离心率为
的离心率为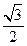 ,
,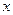 轴被曲线
轴被曲线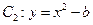 截得的线段长等于
截得的线段长等于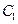 的长半轴长。
的长半轴长。
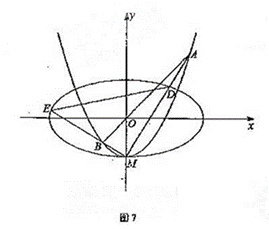
(Ⅰ)求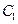 ,
,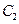 的方程;
的方程;
(Ⅱ)设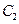 与
与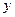 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线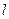 与
与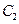 相交于点A,B,直线MA,MB分别与
相交于点A,B,直线MA,MB分别与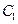 相交与D,E.
相交与D,E.
(i)证明: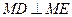 ;
;
(ii)记△MAB,△MDE的面积分别是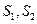 .问:是否存在直线
.问:是否存在直线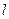 ,使得
,使得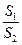 =
=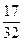 ?
?
请说明理由。
解析:(I)由题意知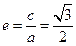 ,从而
,从而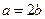 ,又
,又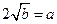 ,解得
,解得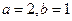 。
。
故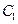 ,
,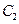 的方程分别为
的方程分别为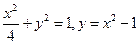 。
。
(II)(i)由题意知,直线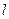 的斜率存在,设为
的斜率存在,设为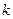 ,则直线
,则直线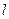 的方程为
的方程为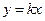 .
.
由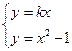 得
得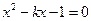 ,
,
设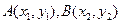 ,则
,则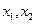 是上述方程的两个实根,于是
是上述方程的两个实根,于是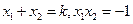 。
。
又点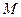 的坐标为
的坐标为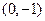 ,所以
,所以
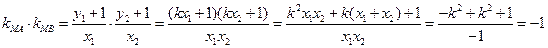
故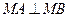 ,即
,即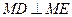 。
。
(ii)设直线的斜率为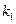 ,则直线的方程为
,则直线的方程为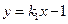 ,由
,由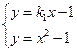 解得
解得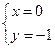 或
或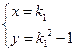 ,则点的坐标为
,则点的坐标为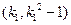
又直线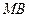 的斜率为
的斜率为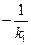 ,同理可得点B的坐标为
,同理可得点B的坐标为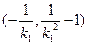 .
.
于是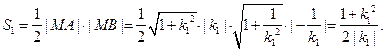
由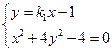 得
得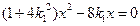 ,
,
解得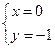 或
或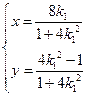 ,则点
,则点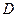 的坐标为
的坐标为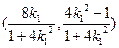 ;
;
又直线的斜率为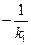 ,同理可得点
,同理可得点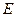 的坐标
的坐标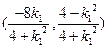
于是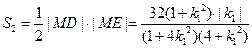
因此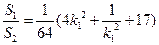
由题意知,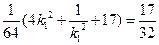 解得
解得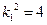 或
或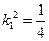 。
。
又由点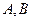 的坐标可知,
的坐标可知,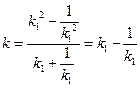 ,所以
,所以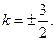
故满足条件的直线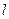 存在,且有两条,其方程分别为
存在,且有两条,其方程分别为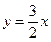 和
和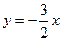 。
。
22.(本小题满分13分)
已知函数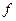 (
(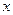 ) =
) =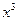 ,g (
,g (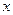 )=
)=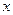 +
+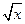 。
。
(Ⅰ)求函数h (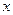 )=
)=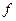 (
(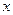 )-g (
)-g (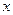 )的零点个数,并说明理由;
)的零点个数,并说明理由;
(Ⅱ)设数列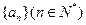 满足
满足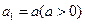 ,
,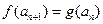 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的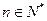 ,都有
,都有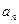 ≤
≤ 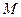 .
.
解析:(I)由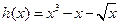 知,
知,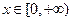 ,而
,而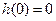 ,且
,且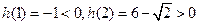 ,则
,则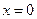 为
为 的一个零点,且
的一个零点,且 在
在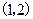 内有零点,因此
内有零点,因此 至少有两个零点
至少有两个零点
解法1: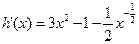 ,记
,记 ,则
,则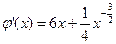 。
。
当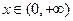 时,
时,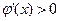 ,因此
,因此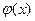 在
在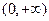 上单调递增,则
上单调递增,则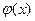 在
在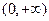 内至多只有一个零点。又因为
内至多只有一个零点。又因为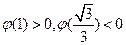 ,则
,则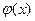 在
在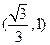 内有零点,所以
内有零点,所以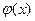 在
在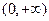 内有且只有一个零点。记此零点为
内有且只有一个零点。记此零点为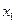 ,则当
,则当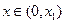 时,
时,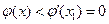 ;当
;当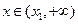 时,
时,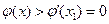 ;
;
所以,
当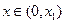 时,
时, 单调递减,而
单调递减,而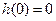 ,则
,则 在
在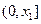 内无零点;
内无零点;
当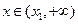 时,
时, 单调递增,则
单调递增,则 在
在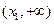 内至多只有一个零点;
内至多只有一个零点;
从而 在
在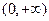 内至多只有一个零点。综上所述,
内至多只有一个零点。综上所述, 有且只有两个零点。
有且只有两个零点。
解法2: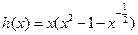 ,记
,记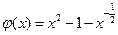 ,则
,则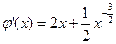 。
。
当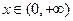 时,
时,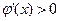 ,因此
,因此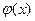 在
在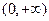 上单调递增,则
上单调递增,则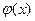 在
在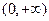 内至多只有一个零点。因此
内至多只有一个零点。因此 在
在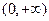 内也至多只有一个零点,
内也至多只有一个零点,
综上所述, 有且只有两个零点。
有且只有两个零点。
(II)记 的正零点为
的正零点为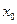 ,即
,即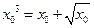 。
。
(1)当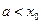 时,由
时,由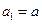 ,即
,即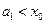 .而
.而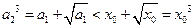 ,因此
,因此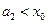 ,由此猜测:
,由此猜测: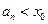 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当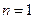 时,
时,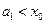 显然成立;
显然成立;
②假设当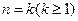 时,有
时,有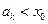 成立,则当
成立,则当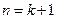 时,由
时,由
 知,
知,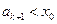 ,因此,当
,因此,当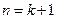 时,
时,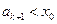 成立。
成立。
故对任意的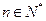 ,
,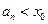 成立。
成立。
(2)当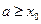 时,由(1)知,
时,由(1)知, 在
在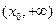 上单调递增。则
上单调递增。则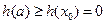 ,即
,即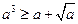 。从而
。从而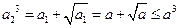 ,即
,即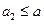 ,由此猜测:
,由此猜测: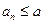 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当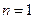 时,
时,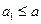 显然成立;
显然成立;
②假设当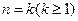 时,有
时,有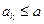 成立,则当
成立,则当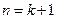 时,由
时,由
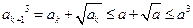 知,
知,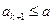 ,因此,当
,因此,当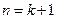 时,
时,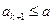 成立。
成立。
故对任意的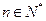 ,
,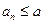 成立。
成立。
综上所述,存在常数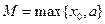 ,使得对于任意的
,使得对于任意的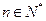 ,都有
,都有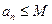 .
.












