三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)在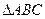 中,角
中,角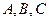 所对的边分别为
所对的边分别为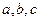 ,且满足
,且满足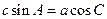 .
.
(I)求角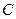 的大小;
的大小;
(II)求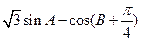 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角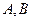 的大小.
的大小.
18. 某商店试销某种商品20天,获得如下数据:
日销售量(件) | 0 | 1 | 2 | 3 |
频数 | 1 | 5 | 9 | 5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
19.(本题满分12分)如图5,在圆锥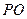 中,已知
中,已知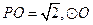 的直径
的直径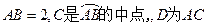 的中点.
的中点.
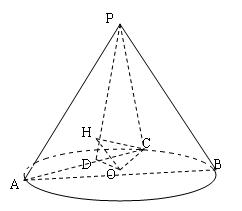
(I)证明: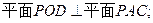
(II)求二面角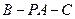 的余弦值.
的余弦值.
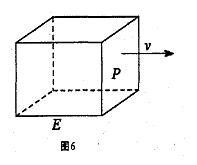
20. 如图6,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为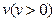 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为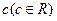 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与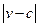 ×S成正比,比例系数为
×S成正比,比例系数为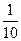 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为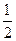 ,记
,记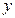 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=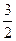 时。
时。
(Ⅰ)写出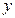 的表达式
的表达式
(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度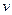 ,使总淋雨量
,使总淋雨量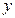 最少。
最少。
解析:(I)由题意知,E移动时单位时间内的淋雨量为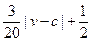 ,
,
故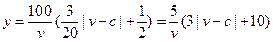 .
.
(II)由(I)知,当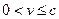 时,
时,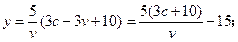
当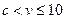 时,
时,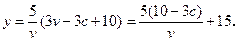
故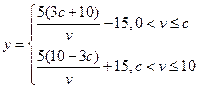 。
。
(1)当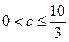 时,
时,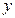 是关于
是关于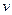 的减函数.故当
的减函数.故当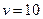 时,
时,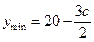 。
。
(2) 当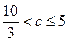 时,在
时,在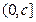 上,
上,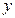 是关于
是关于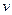 的减函数;在
的减函数;在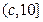 上,
上,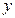 是关于
是关于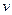 的增函数;故当
的增函数;故当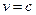 时,
时,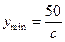 。
。












