一、选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M={-1,0,1},N={x|x2=x},则M∩N=
A.{-1,0,1} B.{0,1} C.{1} D.{0}
【答案】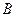
【解析】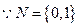 M={-1,0,1}
M={-1,0,1} 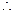 M∩N={0,1}
M∩N={0,1}
【点评】本题考查了集合的基本运算,较简单,易得分.先求出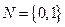 ,再利用交集定义得出M∩N.
,再利用交集定义得出M∩N.
2.复数z=i(i+1)(i为虚数单位)的共轭复数是
A.-1-i B.-1+i C.1-i D.1+i
【答案】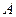
【解析】由z=i(i+1)=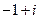 ,及共轭复数定义得
,及共轭复数定义得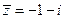 .
.
【点评】本题考查复数代数形式的四则运算及复数的基本概念,考查基本运算能力.先把Z化成标准的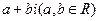 形式,然后由共轭复数定义得出
形式,然后由共轭复数定义得出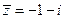 .
.
3.命题“若α=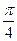 ,则tanα=1”的逆否命题是
,则tanα=1”的逆否命题是
A.若α≠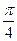 ,则tanα≠1 B. 若α=
,则tanα≠1 B. 若α=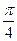 ,则tanα≠1
,则tanα≠1
C. 若tanα≠1,则α≠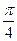 D. 若tanα≠1,则α=
D. 若tanα≠1,则α=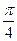
【答案】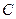
【解析】因为“若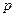 ,则
,则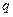 ”的逆否命题为“若
”的逆否命题为“若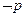 ,则
,则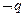 ”,所以 “若α=
”,所以 “若α=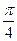 ,则tanα=1”的逆否命题是 “若tanα≠1,则α≠
,则tanα=1”的逆否命题是 “若tanα≠1,则α≠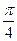 ”.
”.
【点评】本题考查了“若p,则q”形式的命题的逆命题、否命题与逆否命题,考查分析问题的能力.
4.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是
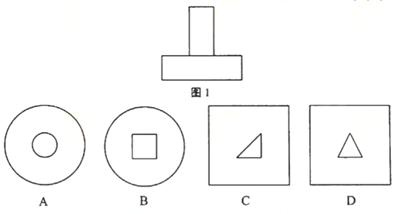
【答案】D
【解析】本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C,都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.

【点评】本题主要考查空间几何体的三视图,考查空间想象能力.是近年来热点题型.
5.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为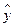 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心(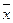 ,
,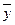 )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
【答案】D
【解析】由回归方程为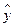 =0.85x-85.71知
=0.85x-85.71知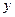 随
随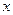 的增大而增大,所以y与x具有正的线性相关关系,由最小二乘法建立的回归方程得过程知
的增大而增大,所以y与x具有正的线性相关关系,由最小二乘法建立的回归方程得过程知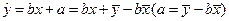 ,所以回归直线过样本点的中心(
,所以回归直线过样本点的中心(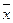 ,
,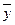 ),利用回归方程可以预测估计总体,所以D不正确.
),利用回归方程可以预测估计总体,所以D不正确.
【点评】本题组要考查两个变量间的相关性、最小二乘法及正相关、负相关的概念,并且是找不正确的答案,易错.
6. 已知双曲线C :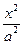 -
-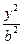 =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A.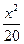 -
-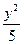 =1 B.
=1 B.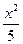 -
-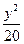 =1 C.
=1 C.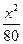 -
-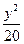 =1 D.
=1 D.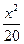 -
-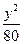 =1
=1
【答案】A
【解析】设双曲线C :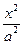 -
-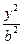 =1的半焦距为
=1的半焦距为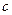 ,则
,则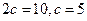 .
.
又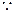 C 的渐近线为
C 的渐近线为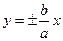 ,点P (2,1)在C 的渐近线上,
,点P (2,1)在C 的渐近线上,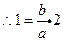 ,即
,即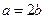 .
.
又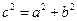 ,
,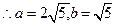 ,
, C的方程为
C的方程为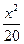 -
-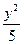 =1.
=1.
【点评】本题考查双曲线的方程、双曲线的渐近线方程等基础知识,考查了数形结合的思想和基本运算能力,是近年来常考题型.
7 . 设 a>b>1,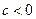 ,给出下列三个结论:
,给出下列三个结论:
① 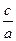 >
>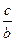 ;②
;② 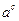 <
<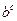 ; ③
; ③ 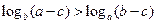 ,
,
其中所有的正确结论的序号是 .
.
A.① B.① ② C.② ③ D.① ②③
【答案】D
【解析】由不等式及a>b>1知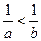 ,又
,又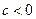 ,所以
,所以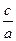 >
>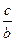 ,①正确;由指数函数的图像与性质知②正确;由a>b>1,
,①正确;由指数函数的图像与性质知②正确;由a>b>1,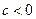 知
知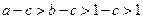 ,由对数函数的图像与性质知③正确.
,由对数函数的图像与性质知③正确.
【点评】本题考查函数概念与基本初等函数Ⅰ中的指数函数的图像与性质、对数函数的图像与性质,不等关系,考查了数形结合的思想.函数概念与基本初等函数Ⅰ是常考知识点.
8 . 在△ABC中,AC=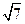 ,BC=2,B =60°,则BC边上的高等于
,BC=2,B =60°,则BC边上的高等于
A.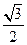 B.
B.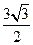 C.
C.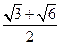 D.
D.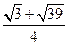
【答案】B
【解析】设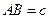 ,在△ABC中,由余弦定理知
,在△ABC中,由余弦定理知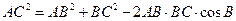 ,
,
即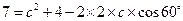 ,
,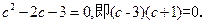 又
又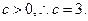
设BC边上的高等于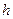 ,由三角形面积公式
,由三角形面积公式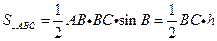 ,知
,知
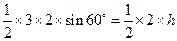 ,解得
,解得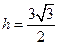 .
.
【点评】本题考查余弦定理、三角形面积公式,考查方程思想、运算能力,是历年常考内容.
9. 设定义在R上的函数f(x)是最小正周期为2π的偶函数,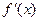 是f(x)的导函数,当
是f(x)的导函数,当
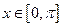 时,0<f(x)<1;当x∈(0,π) 且x≠
时,0<f(x)<1;当x∈(0,π) 且x≠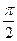 时 ,
时 ,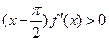 ,则函数y=f(x)-sinx在[-2π,2π] 上的零点个数为
,则函数y=f(x)-sinx在[-2π,2π] 上的零点个数为
A .2 B .4 C.5 D. 8
【答案】B
【解析】由当x∈(0,π) 且x≠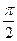 时 ,
时 ,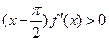 ,知
,知
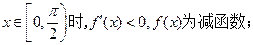
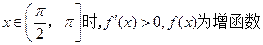
又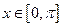 时,0<f(x)<1,在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出
时,0<f(x)<1,在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出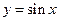 和
和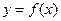 草图像如下,由图知y=f(x)-sinx在[-2π,2π] 上的零点个数为4个.
草图像如下,由图知y=f(x)-sinx在[-2π,2π] 上的零点个数为4个.
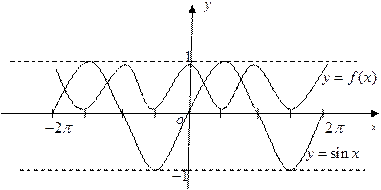

【点评】本题考查函数的周期性、奇偶性、图像及两个图像的交点问题.












