18.(本小题满分12分)
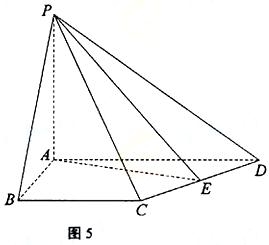
如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
(Ⅰ)证明:CD⊥平面PAE;
(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
【解析】
解法1(Ⅰ如图(1)),连接AC,由AB=4,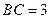 ,
,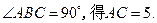
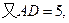 E是CD的中点,所以
E是CD的中点,所以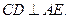
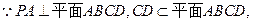 所以
所以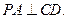
而 内的两条相交直线,所以CD⊥平面PAE.
内的两条相交直线,所以CD⊥平面PAE.
(Ⅱ)过点B作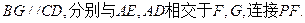
由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是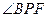 为直线PB与平面PAE
为直线PB与平面PAE
所成的角,且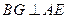 .
.
由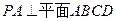 知,
知,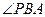 为直线
为直线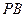 与平面
与平面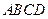 所成的角.
所成的角.
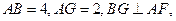 由题意,知
由题意,知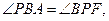
因为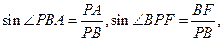 所以
所以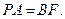
由 所以四边形
所以四边形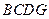 是平行四边形,故
是平行四边形,故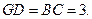 于是
于是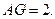
在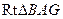 中,
中,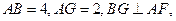 所以
所以
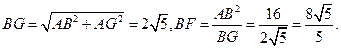
于是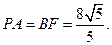
又梯形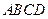 的面积为
的面积为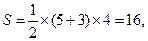 所以四棱锥
所以四棱锥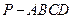 的体积为
的体积为
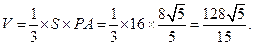
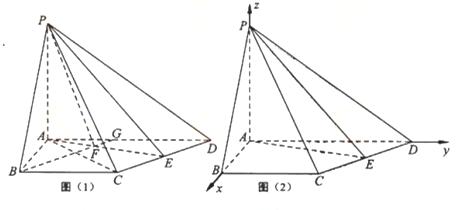
解法2:如图(2),以A为坐标原点,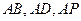 所在直线分别为
所在直线分别为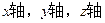 建立空间直角坐标系.设
建立空间直角坐标系.设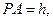 则相关的各点坐标为:
则相关的各点坐标为:
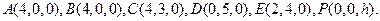
(Ⅰ)易知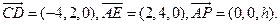 因为
因为
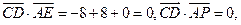 所以
所以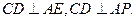 而
而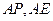 是平面
是平面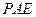 内的两条相交直线,所以
内的两条相交直线,所以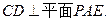
(Ⅱ)由题设和(Ⅰ)知,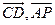 分别是
分别是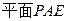 ,
,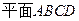 的法向量,而PB与
的法向量,而PB与
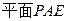 所成的角和PB与
所成的角和PB与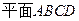 所成的角相等,所以
所成的角相等,所以
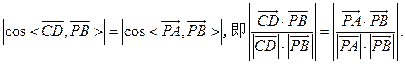
由(Ⅰ)知,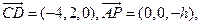 由
由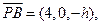 故
故
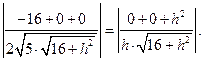
解得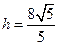 .
.
又梯形ABCD的面积为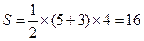 ,所以四棱锥
,所以四棱锥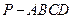 的体积为
的体积为
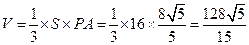 .
.
【点评】本题考查空间线面垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明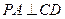 即可,第二问算出梯形的面积和棱锥的高,由
即可,第二问算出梯形的面积和棱锥的高,由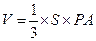 算得体积,或者建立空间直角坐标系,求得高几体积.
算得体积,或者建立空间直角坐标系,求得高几体积.
19.(本小题满分12分)
已知数列{an}的各项均为正数,记A(n)=a1+a2+……+an,B(n)=a2+a3+……+an+1,C(n)=a3+a4+……+an+2,n=1,2,……
(1) 若a1=1,a2=5,且对任意n∈N﹡,三个数A(n),B(n),C(n)组成等差数列,求数列{ an }的通项公式.
(2) 证明:数列{ an }是公比为q的等比数列的充分必要条件是:对任意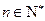 ,三个数A(n),B(n),C(n)组成公比为q的等比数列.
,三个数A(n),B(n),C(n)组成公比为q的等比数列.
【解析】
解(1)对任意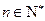 ,三个数
,三个数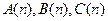 是等差数列,所以
是等差数列,所以
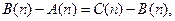
即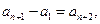 亦即
亦即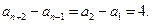
故数列 是首项为1,公差为4的等差数列.于是
是首项为1,公差为4的等差数列.于是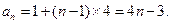
(Ⅱ)(1)必要性:若数列 是公比为q的等比数列,则对任意
是公比为q的等比数列,则对任意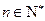 ,有
,有
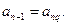 由
由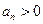 知,
知,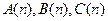 均大于0,于是
均大于0,于是
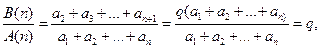
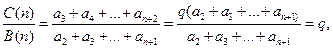
即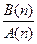 =
=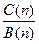 =
=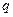 ,所以三个数
,所以三个数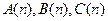 组成公比为
组成公比为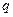 的等比数列.
的等比数列.
(2)充分性:若对于任意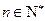 ,三个数
,三个数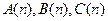 组成公比为
组成公比为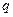 的等比数列,
的等比数列,
则
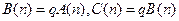 ,
,
于是 得
得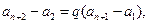 即
即
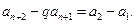
由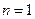 有
有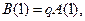 即
即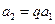 ,从而
,从而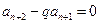 .
.
因为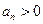 ,所以
,所以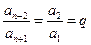 ,故数列
,故数列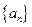 是首项为
是首项为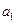 ,公比为
,公比为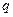 的等比数列,
的等比数列,
综上所述,数列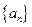 是公比为
是公比为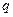 的等比数列的充分必要条件是:对任意n∈N﹡,三个数
的等比数列的充分必要条件是:对任意n∈N﹡,三个数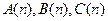 组成公比为
组成公比为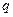 的等比数列.
的等比数列.
【点评】本题考查等差数列、等比数列的定义、性质及充要条件的证明.第一问由等差数列定义可得;第二问要从充分性、必要性两方面来证明,利用等比数列的定义及性质易得证.
20.(本小题满分13分)
某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
【解析】
解:(Ⅰ)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为
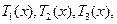 由题设有
由题设有
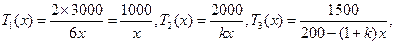
期中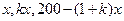 均为1到200之间的正整数.
均为1到200之间的正整数.
(Ⅱ)完成订单任务的时间为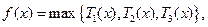 其定义域为
其定义域为
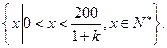 易知,
易知,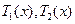 为减函数,
为减函数,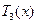 为增函数.注意到
为增函数.注意到
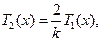 于是
于是
(1)当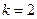 时,
时,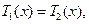 此时
此时
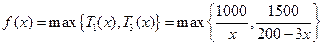 ,
,
由函数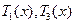 的单调性知,当
的单调性知,当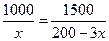 时
时 取得最小值,解得
取得最小值,解得
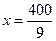 .由于
.由于
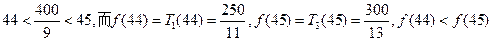 .
.
故当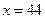 时完成订单任务的时间最短,且最短时间为
时完成订单任务的时间最短,且最短时间为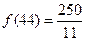 .
.
(2)当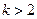 时,
时,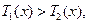 由于
由于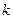 为正整数,故
为正整数,故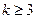 ,此时
,此时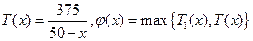 易知
易知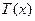 为增函数,则
为增函数,则
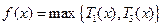
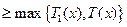
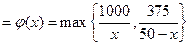 .
.
由函数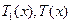 的单调性知,当
的单调性知,当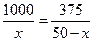 时
时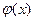 取得最小值,解得
取得最小值,解得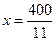 .由于
.由于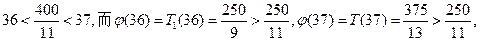
此时完成订单任务的最短时间大于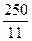 .
.
(3)当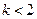 时,
时,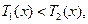 由于
由于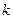 为正整数,故
为正整数,故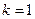 ,此时
,此时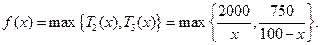 由函数
由函数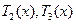 的单调性知,
的单调性知,
当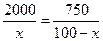 时
时 取得最小值,解得
取得最小值,解得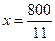 .类似(1)的讨论.此时
.类似(1)的讨论.此时
完成订单任务的最短时间为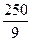 ,大于
,大于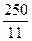 .
.
综上所述,当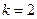 时完成订单任务的时间最短,此时生产A,B,C三种部件的人数
时完成订单任务的时间最短,此时生产A,B,C三种部件的人数
分别为44,88,68.
【点评】本题为函数的应用题,考查分段函数、函数单调性、最值等,考查运算能力及用数学知识分析解决实际应用问题的能力.第一问建立函数模型;第二问利用单调性与最值来解决,体现分类讨论思想.
21.(本小题满分13分)
在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(Ⅰ)求曲线C1的方程;
(Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
【解析】(Ⅰ)解法1 :设M的坐标为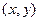 ,由已知得
,由已知得
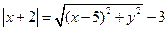 ,
,
易知圆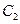 上的点位于直线
上的点位于直线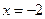 的右侧.于是
的右侧.于是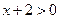 ,所以
,所以
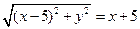 .
.
化简得曲线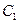 的方程为
的方程为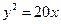 .
.
解法2 :由题设知,曲线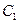 上任意一点M到圆心
上任意一点M到圆心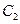
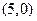 的距离等于它到直线
的距离等于它到直线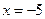 的距离,因此,曲线
的距离,因此,曲线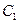 是以
是以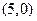 为焦点,直线
为焦点,直线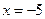 为准线的抛物线,故其方程为
为准线的抛物线,故其方程为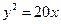 .
.
(Ⅱ)当点P在直线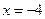 上运动时,P的坐标为
上运动时,P的坐标为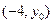 ,又
,又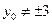 ,则过P且与圆
,则过P且与圆
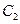 相切得直线的斜率
相切得直线的斜率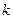 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为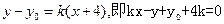 .于是
.于是
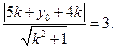
整理得
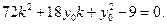 ①
①
设过P所作的两条切线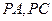 的斜率分别为
的斜率分别为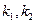 ,则
,则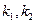 是方程①的两个实根,故
是方程①的两个实根,故
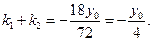 ②
②
由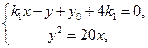 得
得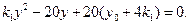 ③
③
设四点A,B,C,D的纵坐标分别为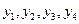 ,则是方程③的两个实根,所以
,则是方程③的两个实根,所以
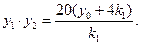 ④
④
同理可得
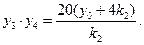 ⑤
⑤
于是由②,④,⑤三式得
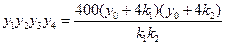
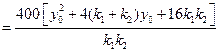
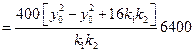 .
.
所以,当P在直线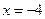 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.
【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问用直接法或定义法求出曲线的方程;第二问设出切线方程,把直线与曲线方程联立,由一元二次方程根与系数的关系得到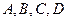 四点纵坐标之积为定值,体现“设而不求”思想.
四点纵坐标之积为定值,体现“设而不求”思想.
22.(本小题满分13分)
已知函数 =
=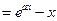 ,其中a≠0.
,其中a≠0.
(1) 若对一切x∈R, ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函数 的图像上取定两点
的图像上取定两点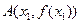 ,
,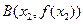
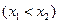 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使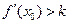 成立?若存在,求
成立?若存在,求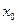 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【解析】(Ⅰ)若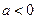 ,则对一切
,则对一切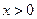 ,
,
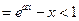 ,这与题设矛盾,又
,这与题设矛盾,又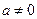 ,
,
故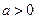 .
.
而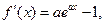 令
令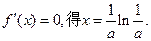
当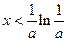 时,
时,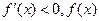 单调递减;当
单调递减;当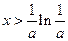 时,
时,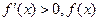 单调递增,故当
单调递增,故当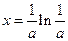 时,
时, 取最小值
取最小值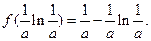
于是对一切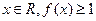 恒成立,当且仅当
恒成立,当且仅当
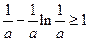 . ①
. ①
令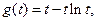 则
则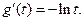
当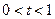 时,
时,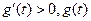 单调递增;当
单调递增;当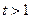 时,
时,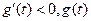 单调递减.
单调递减.
故当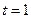 时,
时,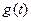 取最大值
取最大值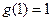 .因此,当且仅当
.因此,当且仅当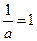 即
即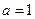 时,①式成立.
时,①式成立.
综上所述,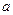 的取值集合为
的取值集合为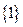 .
.
(Ⅱ)由题意知,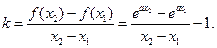
令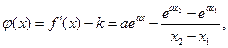 则
则
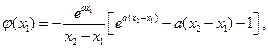
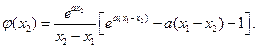
令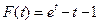 ,则
,则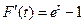 .
.
当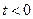 时,
时,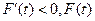 单调递减;当
单调递减;当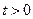 时,
时,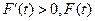 单调递增.
单调递增.
故当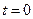 ,
,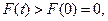 即
即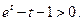
从而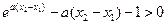 ,
,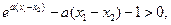 又
又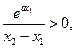
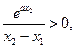
所以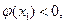
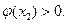
因为函数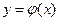 在区间
在区间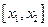 上的图像是连续不断的一条曲线,所以存在
上的图像是连续不断的一条曲线,所以存在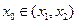 使
使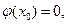
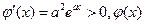 单调递增,故这样的
单调递增,故这样的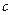 是唯一的,且
是唯一的,且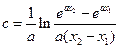 .故当且仅当
.故当且仅当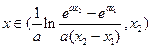 时,
时, 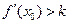 .
.
综上所述,存在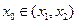 使
使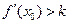 成立.且
成立.且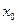 的取值范围为
的取值范围为
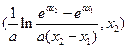 .
.
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想,转化与划归思想等数学思想方法.第一问利用导函数法求出 取最小值
取最小值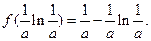 对一切x∈R,f(x)
对一切x∈R,f(x) 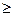 1恒成立转化为
1恒成立转化为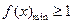 ,从而得出a的取值集合;第二问在假设存在的情况下进行推理,通过构造函数,研究这个函数的单调性及最值来进行分析判断.
,从而得出a的取值集合;第二问在假设存在的情况下进行推理,通过构造函数,研究这个函数的单调性及最值来进行分析判断.