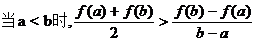17. (本小题满分12分)
设Sn表示数列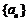 的前n项和.
的前n项和.
(Ⅰ) 若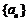 为等差数列, 推导Sn的计算公式;
为等差数列, 推导Sn的计算公式;
(Ⅱ) 若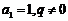 , 且对所有正整数n, 有
, 且对所有正整数n, 有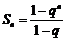 . 判断
. 判断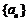 是否为等比数列.
是否为等比数列.
17. 【答案】(Ⅰ) 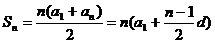 ;
;
(Ⅱ) 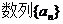 是首项
是首项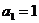 ,公比
,公比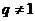 的等比数列。
的等比数列。
【解析】(Ⅰ) 设公差为d,则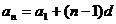
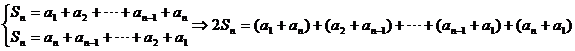
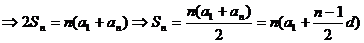 .
.
(Ⅱ) 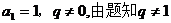 。
。
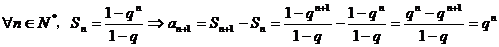
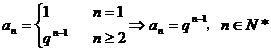 .
.
所以,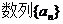 是首项
是首项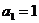 ,公比
,公比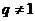 的等比数列。
的等比数列。
18. (本小题满分12分)
如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, 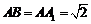 .
.
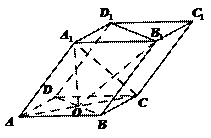
(Ⅰ) 证明: A1BD // 平面CD1B1;
(Ⅱ) 求三棱柱ABD-A1B1D1的体积.
18. 【答案】 (Ⅰ) 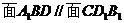 ,见下.
,见下.
(Ⅱ) 1
【解析】 (Ⅰ) 设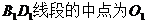 .
.
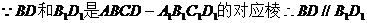 .
.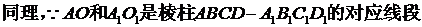
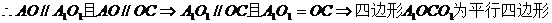
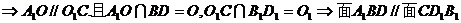 .(证毕)
.(证毕)
(Ⅱ) 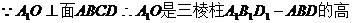 .
.
在正方形AB CD中,AO = 1 . 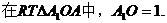
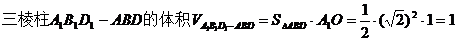 .
.
所以,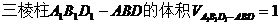 .
.
19. (本小题满分12分)
有7位歌手(1至7号)参加一场歌唱比赛, 由500名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组, 各组的人数如下:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
(Ⅰ) 为了调查评委对7位歌手的支持状况, 现用分层抽样方法从各组中抽取若干评委, 其中从B组中抽取了6人. 请将其余各组抽取的人数填入下表.
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | 6 |
(Ⅱ) 在(Ⅰ)中, 若A, B两组被抽到的评委中各有2人支持1号歌手, 现从这两组被抽到的评委中分别任选1人, 求这2人都支持1号歌手的概率.
19. 【答案】 (Ⅰ).
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | 3 | 6 | 9 | 9 | 3 |
(Ⅱ) 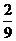
【解析】 (Ⅰ) 按相同的比例从不同的组中抽取人数。
从B组100人中抽取6人,即从50人中抽取3人,从100人中抽取6人,从100人中抽取9人。
(Ⅱ) A组抽取的3人中有2人支持1号歌手,则从3人中任选1人,支持支持1号歌手的概率为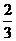 ·
·
B组抽取的6人中有2人支持1号歌手,则从6人中任选1人,支持支持1号歌手的概率为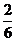 ·
·
现从抽样评委A组3人,B组6人中各自任选一人,则这2人都支持1号歌手的概率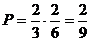 .
.
所以,从A,B两组抽样评委中,各自任选一人,则这2人都支持1号歌手的概率为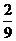 .
.
20. (本小题满分13分)
已知动点M(x,y)到直线l:x = 4的距离是它到点N(1,0)的距离的2倍.
(Ⅰ) 求动点M的轨迹C的方程;
(Ⅱ) 过点P(0,3)的直线m与轨迹C交于A, B两点. 若A是PB的中点, 求直线m的斜率.
20. 【答案】 (Ⅰ).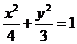 .(Ⅱ)
.(Ⅱ) 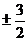
【解析】 (Ⅰ) 点M(x,y)到直线x=4的距离,是到点N(1,0)的距离的2倍,则
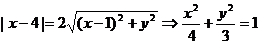 .
.
所以,动点M的轨迹为 椭圆,方程为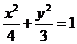
(Ⅱ) P(0, 3), 设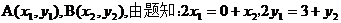
椭圆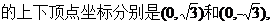 经检验直线m不经过这2点,即直线m斜率k存在。
经检验直线m不经过这2点,即直线m斜率k存在。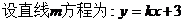 .联立椭圆和直线方程,整理得:
.联立椭圆和直线方程,整理得:
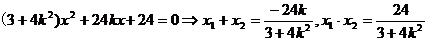
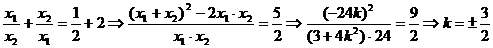
所以,直线m的斜率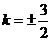
21. (本小题满分14分)
已知函数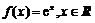 .
.
(Ⅰ) 求f(x)的反函数的图象上图象上点(1,0)处的切线方程;
(Ⅱ) 证明: 曲线y = f (x) 与曲线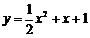 有唯一公共点.
有唯一公共点.
(Ⅲ) 设a<b, 比较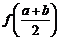 与
与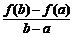 的大小, 并说明理由.
的大小, 并说明理由.
21. 【答案】(Ⅰ) y = x+ 1.
当m 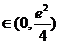 时,有0个公共点;当m=
时,有0个公共点;当m= 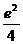 ,有1个公共点;当m
,有1个公共点;当m 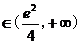 有2个公共点;
有2个公共点;
(Ⅲ) 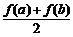 >
> 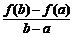
(Ⅱ)【解析】(Ⅰ) f (x)的反函数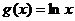 ,则y=g(x)过点(1,0)的切线斜率k=
,则y=g(x)过点(1,0)的切线斜率k=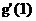 .
.
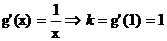 .过点(1,0)的切线方程为:y = x+ 1
.过点(1,0)的切线方程为:y = x+ 1
(Ⅱ) 证明曲线y=f(x)与曲线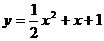 有唯一公共点,过程如下。
有唯一公共点,过程如下。
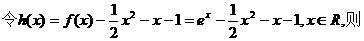
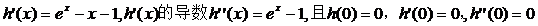
因此,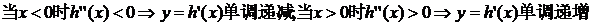
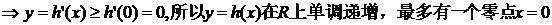
所以,曲线y=f(x)与曲线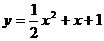 只有唯一公共点(0,1).(证毕)
只有唯一公共点(0,1).(证毕)
(Ⅲ) 设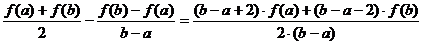
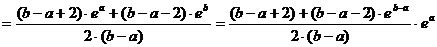
令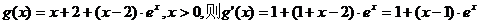 。
。
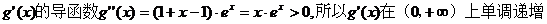 ,且
,且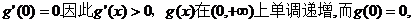
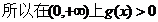 。
。
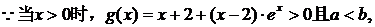
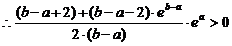
所以