20.(本小题满分12分)
已知函数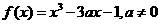
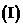 求
求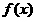 的单调区间;
的单调区间;
 若
若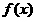 在
在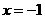 处取得极值,直线y=m与
处取得极值,直线y=m与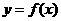 的图象有三个不同的交点,求m的取值范围。
的图象有三个不同的交点,求m的取值范围。
解:(1)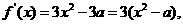
当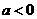 时,对
时,对 ,有
,有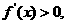
 当
当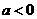 时,
时,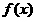 的单调增区间为
的单调增区间为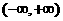
当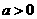 时,由
时,由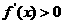 解得
解得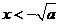 或
或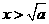 ;
;
由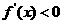 解得
解得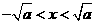 ,
,
 当
当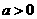 时,
时,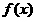 的单调增区间为
的单调增区间为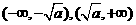 ;
;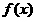 的单调减区间为
的单调减区间为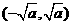 。
。
(2)
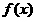 在
在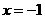 处取得极大值,
处取得极大值,
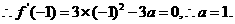

由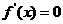 解得
解得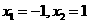 。
。
由(1)中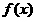 的单调性可知,
的单调性可知,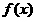 在
在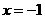 处取得极大值
处取得极大值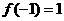 ,
,
在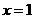 处取得极小值
处取得极小值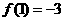 。
。
 直线
直线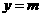 与函数
与函数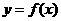 的图象有三个不同的交点,又
的图象有三个不同的交点,又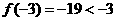 ,
,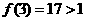 ,
,
结合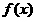 的单调性可知,
的单调性可知, 的取值范围是
的取值范围是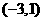 。
。
21.(本小题满分12分)
已知数列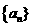 满足,
满足, 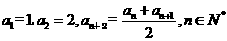 .
.
 令
令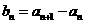 ,证明:
,证明: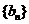 是等比数列;
是等比数列;
(Ⅱ)求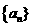 的通项公式。
的通项公式。
(1)证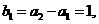
当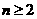 时,
时,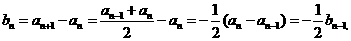
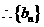 是以1为首项,
是以1为首项,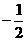 为公比的等比数列。
为公比的等比数列。
(2)解由(1)知
当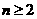 时,
时,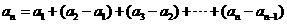
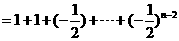
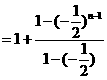
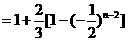
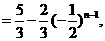
当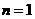 时,
时,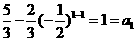 。
。
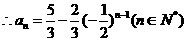 。
。
22.(本小题满分12分)
已知双曲线C的方程为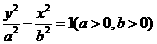 ,离心率
,离心率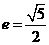 ,顶点到渐近线的距离为
,顶点到渐近线的距离为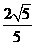 。
。
(I) 求双曲线C的方程;
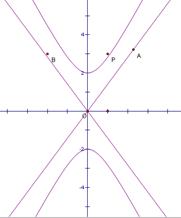
(II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若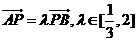 ,求
,求 面积的取值范围
面积的取值范围
解答一(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线 ,
,
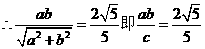
由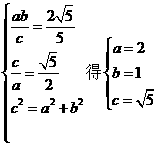

(Ⅱ)由(Ⅰ)知双曲线C的两条渐近线方程为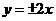
设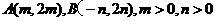
由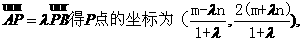
将P点的坐标代入
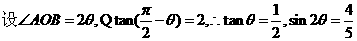
又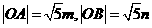
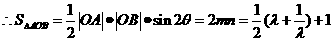
记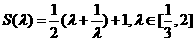
则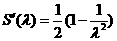
由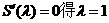
又S(1)=2,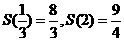


解答二(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线 ,
,
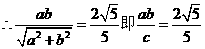
由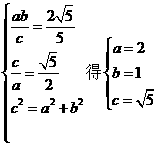

(Ⅱ)设直线AB的方程为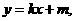
由题意知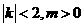
由
由
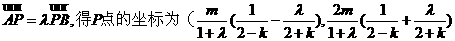
将P点的坐标代入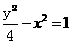 得
得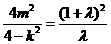
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m)
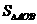 =
=
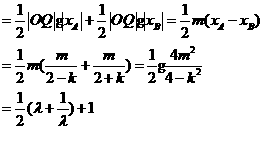
以下同解答一