23．（2013安顺）如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．

（1）求证：四边形BCFE是菱形；

（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．

考点：菱形的判定与性质；三角形中位线定理．

分析：从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；∠BCF是120°，所以∠EBC为60°，所以菱形的边长也为4，求出菱形的高面积就可求．

解答：（1）证明：∵D、E分别是AB、AC的中点，

∴DE∥BC且2DE=BC，

又∵BE=2DE，EF=BE，

∴EF=BC，EF∥BC，

∴四边形BCFE是平行四边形，

又∵BE=FE，

∴四边形BCFE是菱形；

（2）解：∵∠BCF=120°，

∴∠EBC=60°，

∴△EBC是等边三角形，

∴菱形的边长为4，高为2，

∴菱形的面积为4×2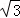=8．

点评：本题考查菱形的判定和性质以及三角形中位线定理，以及菱形的面积的计算等知识点．　

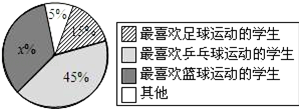
24．（2013安顺）某校一课外活动小组为了解学生最喜欢的球类运动情况，随机抽查本校九年级的200名学生，调查的结果如图所示．请根据该扇形统计图解答以下问题：（1）求图中的x的值；

（2）求最喜欢乒乓球运动的学生人数；

（3）若由3名最喜欢篮球运动的学生，1名最喜欢乒乓球运动的学生，1名最喜欢足球运动的学生组队外出参加一次联谊活动．欲从中选出2人担任组长（不分正副），列出所有可能情况，并求2人均是最喜欢篮球运动的学生的概率．

考点：扇形统计图；概率公式．

专题：图表型．

分析：（1）考查了扇形图的性质，注意所有小扇形的百分数和为1；

（2）根据扇形图求解，解题的关键是找到对应量：最喜欢乒乓球运动的学生人数对应的百分比为x%；

（3）此题可以采用列举法，注意要做到不重不漏．

解答：解：（1）由题得：x%+5%+15%+45%=1，

解得：x=35．（2分）

（2）最喜欢乒乓球运动的学生人数为200×45%=90（人）．（4分）

（3）用A1，A2，A3表示3名最喜欢篮球运动的学生，B表示1名最喜欢乒乓球运动的学生，C表示1名喜欢足球运动的学生，则从5人中选出2人的情况有：（A1，A2），（A1，A3），（A1，B），（A1，C），（A2，A3），（A2，B），（A2，C），（A3，B），（A3，C），（B，C），共计10种．（6分）

选出的2人都是最喜欢篮球运动的学生的有（A1，A2），（A1，A3），（A2，A3）共计3种，（7分）

则选出2人都最喜欢篮球运动的学生的概率为．（9分）

点评：此题考查了扇形图与概率的知识，综合性比较强，解题时要注意认真审题，理解题意；在用列举法求概率时，一定要注意不重不漏．用到的知识点为：概率=所求情况数与总情况数之比．　

25．（2013安顺）如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．

（1）求证：CT为⊙O的切线；

（2）若⊙O半径为2，CT=，求AD的长．

考点：切线的判定与性质；勾股定理；圆周角定理．

分析：（1）连接OT，根据角平分线的性质，以及直角三角形的两个锐角互余，证得CT⊥OT，CT为⊙O的切线；

（2）证明四边形OTCE为矩形，求得OE的长，在直角△OAE中，利用勾股定理即可求解．

解答：（1）证明：连接OT，

∵OA=OT，

∴∠OAT=∠OTA，

又∵AT平分∠BAD，

∴∠DAT=∠OAT，

∴∠DAT=∠OTA，

∴OT∥AC，（3分）

又∵CT⊥AC，

∴CT⊥OT，

∴CT为⊙O的切线；（5分）

（2）解：过O作OE⊥AD于E，则E为AD中点，

又∵CT⊥AC，

∴OE∥CT，

∴四边形OTCE为矩形，（7分）

∵CT=，

∴OE=，

又∵OA=2，

∴在Rt△OAE中，，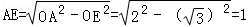

∴AD=2AE=2．（10分）

点评：本题主要考查了切线的判定以及性质，证明切线时可以利用切线的判定定理把问题转化为证明垂直的问题．　

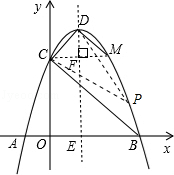
26．（2013安顺）如图，已知抛物线与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C（0，3）．

（1）求抛物线的解析式；

（2）设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；

（3）点M是抛物线上一点，以B，C，D，M为顶点的四边形是直角梯形，试求出点M的坐标．

考点：二次函数综合题．

专题：压轴题．

分析：（1）由于A（﹣1，0）、B（3，0）、C（0，3）三点均在坐标轴上，故设一般式解答和设交点式（两点式）解答均可．

（2）分以CD为底和以CD为腰两种情况讨论．运用两点间距离公式建立起P点横坐标和纵坐标之间的关系，再结合抛物线解析式即可求解．

（3）根据抛物线上点的坐标特点，利用勾股定理求出相关边长，再利用勾股定理的逆定理判断出直角梯形中的直角，便可解答．

解答：解：（1）∵抛物线与y轴交于点C（0，3），

∴设抛物线解析式为y=ax2+bx+3（a≠0），

根据题意，得，

解得，

∴抛物线的解析式为y=﹣x2+2x+3．

（2）存在．

由y=﹣x2+2x+3得，D点坐标为（1，4），对称轴为x=1．

①若以CD为底边，则PD=PC，

设P点坐标为（x，y），根据两点间距离公式，

得x2+（3﹣y）2=（x﹣1）2+（4﹣y）2，

即y=4﹣x．

又P点（x，y）在抛物线上，

∴4﹣x=﹣x2+2x+3，

即x2﹣3x+1=0，

解得x1=，x2=＜1，应舍去，

∴x=，

∴y=4﹣x=，

即点P坐标为．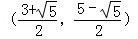

②若以CD为一腰，

∵点P在对称轴右侧的抛物线上，由抛物线对称性知，点P与点C关于直线x=1对称，

此时点P坐标为（2，3）．

∴符合条件的点P坐标为或（2，3）．

（3）由B（3，0），C（0，3），D（1，4），根据勾股定理，

得CB=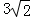，CD=，BD=，

∴CB2+CD2=BD2=20，

∴∠BCD=90°，

设对称轴交x轴于点E，过C作CM⊥DE，交抛物线于点M，垂足为F，在Rt△DCF中，

∵CF=DF=1，

∴∠CDF=45°，

由抛物线对称性可知，∠CDM=2×45°=90°，点坐标M为（2，3），

∴DM∥BC，

∴四边形BCDM为直角梯形，

由∠BCD=90°及题意可知，

以BC为一底时，顶点M在抛物线上的直角梯形只有上述一种情况；

以CD为一底或以BD为一底，且顶点M在抛物线上的直角梯形均不存在．

综上所述，符合条件的点M的坐标为（2，3）．

点评：此题是一道典型的“存在性问题”，结合二次函数图象和等腰三角形、等腰梯形的性质，考查了它们存在的条件，有一定的开放性．　

点击此处下载文档(rar格式，125.45KB)