第Ⅰ卷
一、选择题
(1)复数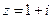 ,
,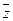 为
为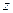 的共轭复数,则
的共轭复数,则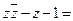
(A)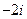 (B)
(B)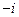 (C)
(C)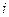 (D)
(D)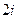
【答案】B
【命题意图】本题主要考查复数的运算.
【解析】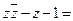 |z|
|z|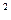
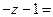 2-(1+i)-1=
2-(1+i)-1=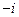 .
.
(2)函数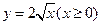 的反函数为
的反函数为
(A)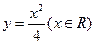 (B)
(B)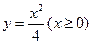
(C)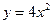
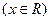 (D)
(D)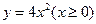
【答案】B
【命题意图】本题主要考查反函数的求法.
【解析】由原函数反解得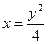 ,又原函数的值域为
,又原函数的值域为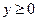 ,所以函数
,所以函数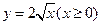 的反函数为
的反函数为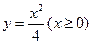 .
.
(3)下面四个条件中,使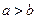 成立的充分而不必要的条件是
成立的充分而不必要的条件是
(A)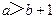 (B)
(B)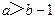 (C)
(C)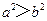 (D)
(D)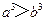
【答案】A
【命题意图】本题主要考查充要条件及不等式的性质.
【解析】即寻找命题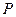 ,使
,使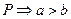 ,且
,且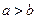 推不出
推不出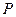 ,逐项验证知可选A.
,逐项验证知可选A.
(4)设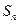 为等差数列
为等差数列
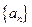 的前
的前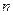 项和,若
项和,若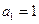 ,公差
,公差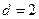 ,
,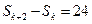 ,则
,则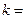
(A)8 (B)7 (C)6 (D)5
【答案】D
【命题意图】本题主要考查等差数列的基本公式的应用.
【解析】解法一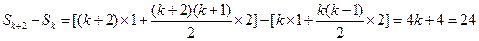 ,解得
,解得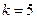 .
.
解法二: 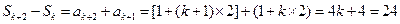 ,解得
,解得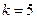 .
.
(5)设函数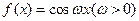 ,将
,将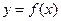 的图像向右平移
的图像向右平移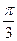 个单位长度后,所得的图像与原图像重合,则
个单位长度后,所得的图像与原图像重合,则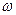 的最小值等于
的最小值等于
(A)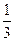 (B)
(B)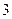 (C)
(C)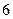 (D)
(D)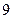
【答案】C
【命题意图】本题主要考查三角函数的周期性及三角函数图像的平移变换.
【解析】由题意得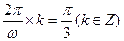 ,解得
,解得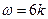 ,又
,又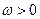 ,令
,令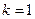 ,得
,得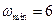 .
.
(6)已知直二面角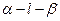 ,点
,点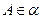 ,
,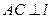 ,
,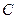 为垂足,
为垂足,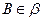 ,
,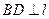 ,
,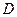 为垂
为垂
足.若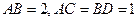 ,则
,则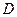 到平面
到平面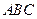 的距离等于
的距离等于
(A)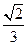 (B)
(B)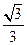 (C)
(C)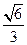 (D) 1
(D) 1
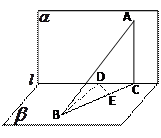
【答案】C
【命题意图】本题主要考查空间点到平面距离的求法.
【解析】如图,过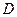 作
作 ,垂足为
,垂足为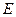 ,因为
,因为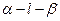 是直二面角,
是直二面角, 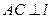 ,∴
,∴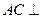 平面
平面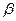 ,
,
∴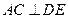 ,
,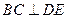 ,
,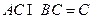 ,∴
,∴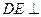 平面
平面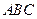 ,故
,故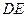 的长为点
的长为点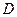 到平面
到平面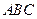 的距离.在
的距离.在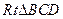 中,由等面积法得
中,由等面积法得 .
.
(7)某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友每位朋友1本,则不同的赠送方法共有
(A)4种 (B)10种 (C)18种 (D)20种
【答案】B
【命题意图】本题主要考查两个原理与排列组合知识,考察考生分析问题的能力.
【解析】分两类:一是取出1本画册,3本集邮册,此时赠送方法有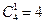 种;
种;
二是取出2本画册,2本集邮册,此时赠送方法有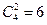 种.故赠送方法共有10
种.故赠送方法共有10 种.
种.
(8)曲线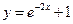 在点(0,2)处的切线与直线
在点(0,2)处的切线与直线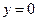 和
和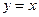 围
围 成的三角形的面积为
成的三角形的面积为
(A)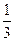 (B)
(B)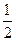 (C)
(C)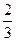 (D)1
(D)1
【答案】A
【命题意图】本题主要考查利用导数求切线方程和三角形面积公式.
【解析】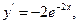 ∴曲线
∴曲线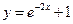 在点(0,2)处的切线的斜率
在点(0,2)处的切线的斜率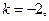 故切线方程是
故切线方程是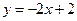 ,在直角坐标系中作出示意图得围
,在直角坐标系中作出示意图得围 成的三角形的三个顶点分别为(0,0)、(1,0)、(
成的三角形的三个顶点分别为(0,0)、(1,0)、(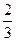 ,
, 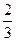 ),∴三角形的面积是
),∴三角形的面积是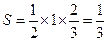 .
.
(9)设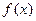 是周期为2的奇函数,当
是周期为2的奇函数,当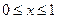 时,
时,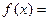
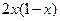 ,则
,则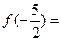
(A) -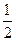 (B)
(B)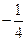 (C)
(C)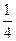 (D)
(D)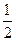
【答案】A
【命题意图】本题主要考查利用函数的周期性和奇偶性求函数值的方法.
【解析】由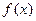 是周期为2的奇函数,利用周期性和奇偶性得:
是周期为2的奇函数,利用周期性和奇偶性得: 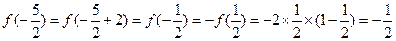 .
.
(10)已知抛物线C: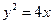 的焦点为
的焦点为 ,直线
,直线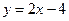 与
与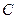 交于
交于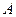 ,
,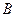 两点.则
两点.则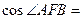
(A)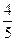 (B)
(B)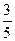 (C)
(C)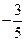 (D)
(D)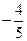
【答案】D
【命题意图】本题主要考查直线与抛物线的位置关系,余弦定理的应用.
【解析】联立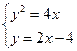 消去
消去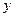 得
得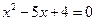 ,解得
,解得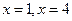 ,不妨设
,不妨设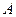 点在
点在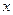 轴的上方,于是
轴的上方,于是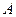 ,
,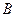 两点的坐标分别为(4,4),(1,
两点的坐标分别为(4,4),(1,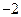 ),又
),又 ,可求得
,可求得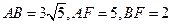 .在
.在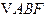 中,由余弦定理
中,由余弦定理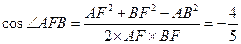 .
.
(11)已知平面α截一球面得圆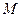 ,过圆心
,过圆心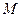 且与α成
且与α成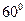 二面角的平面β截该球面得圆
二面角的平面β截该球面得圆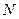 .若该球面的半径为4,圆
.若该球面的半径为4,圆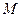 的面积为4
的面积为4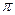 ,则圆
,则圆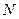 的面积为
的面积为
(A)7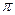 (B)9
(B)9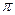 (C)11
(C)11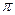 (D)13
(D)13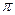
【答案】D
【命题意图】本题主要考查二面角的概念与球的性质.
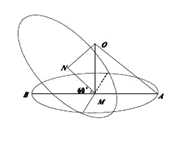
【解析】如图所示,由圆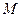 的面积为4
的面积为4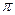 知球心
知球心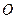 到圆
到圆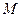 的距离
的距离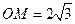 ,在
,在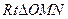 中,
中,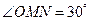 , ∴
, ∴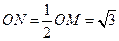 ,故圆
,故圆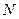 的半径
的半径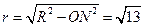 ,∴圆
,∴圆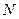 的面积为
的面积为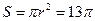 .
.
(12)设向量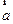 ,
,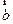 ,
,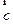 满足|
满足|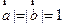 ,
,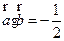 ,
,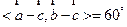 ,则
,则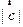 的最大值等于
的最大值等于
(A)2 (B)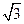
 (c)
(c)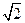 (D)1
(D)1
【答案】A
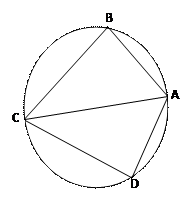
【命题意图】本题主要考查平面向量的数量积运算、向量加减法、四点共圆的条件及数形结合的思想.
【解析】如图,设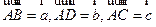 ,则
,则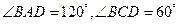 ,
,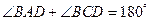 ,∴
,∴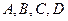 四点共圆,当
四点共圆,当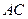 为圆的直径时,
为圆的直径时,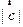 最大,最大值为2.
最大,最大值为2.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上(注意:在试卷上作答无效)
(13)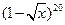 的二项展开式中,
的二项展开式中,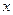 的系数与
的系数与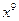 的系数之差为
的系数之差为  .
.
【答案】0
【命题意图】本题主要考查二项展开式的通项公式和组合数的性质.
【解析】由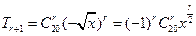 得
得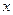 的系数为
的系数为 ,
,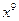 的系数为
的系数为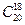 ,而
,而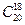 =
= ,所以
,所以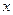 的系数与
的系数与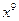 的系数之差为0.
的系数之差为0.
(14)已知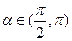 ,
,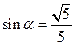 ,则
,则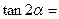
 .
.
【答案】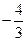
【命题意图】本题主要考查同角三角函数的基本关系和二倍角的正切公式.
【解析】由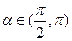 ,
,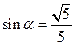 得
得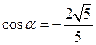 ,故
,故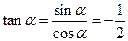 ,
,
∴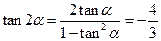 .
.
(15)已知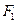 、
、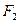 分别为双曲线
分别为双曲线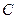 :
: 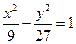 的左、右焦点,点
的左、右焦点,点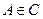 ,点
,点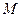 的坐标为(2,0),
的坐标为(2,0),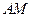 为
为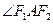 的平分线.则
的平分线.则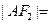 .
.
【答案】6
【命题意图】本题主要考查三角形的内角平分线定理,双曲线的第一定义和性质.
【解析】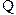
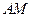 为
为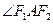 的平分线,∴
的平分线,∴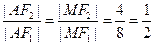 ∴
∴
又点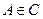 ,由双曲线的第一定义得
,由双曲线的第一定义得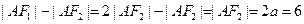 .
.
(16)己知点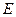 、
、 分别在正方体
分别在正方体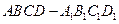 的棱
的棱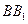 、
、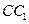 上,且
上,且 ,则面
,则面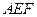 与面
与面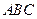 所成的二面角的正切值等于 .
所成的二面角的正切值等于 .
【答案】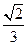
【命题意图】本题主要考查正方体中二面角的求法.
【解析】延长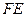 交
交 的延长线于
的延长线于 ,连结
,连结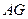 ,则
,则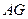 为面
为面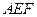 与面
与面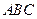 的交线,由
的交线,由 得
得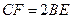 ,∴
,∴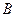 为
为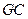 中点.设正方体的棱长为1,则
中点.设正方体的棱长为1,则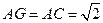 ,又
,又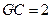 ,∴
,∴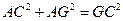 ∴
∴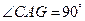
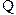
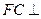 平面
平面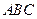 ,∴
,∴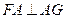 ∴
∴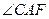 是面
是面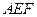 与面
与面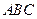 所成的二面角的平面角,在
所成的二面角的平面角,在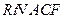 中,
中,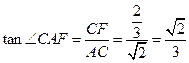 ,故面
,故面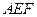 与面
与面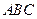 所成的二面角的正切值等于
所成的二面角的正切值等于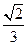 .
.












