三、解答题(本大题共6个小题,共74分。解答应写出必要的文字说明,证明过程或演算步骤。)
17、(本小题满分12分) 某居民小区有两个相互独立的安全防范系统(简称系统)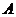 和
和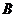 ,系统
,系统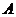 和系统
和系统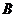 在任意时刻发生故障的概率分别为
在任意时刻发生故障的概率分别为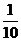 和
和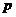 。
。
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为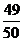 ,求
,求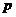 的值;
的值;
(Ⅱ)求系统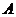 在3次相互独立的检测中不发生故障的次数大于发生故障的次数的概率。
在3次相互独立的检测中不发生故障的次数大于发生故障的次数的概率。
[解析](1)设:“至少有一个系统不发生故障”为事件C,那么
1-P(C)=1-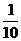 P=
P=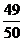 ,解得P=
,解得P=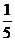 ………………………………6 分
………………………………6 分
(2)设“系统A在3次相互独立的检测中不发生故障的次数大于发生故障的次数”为
事件D,
那么P(D)=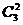

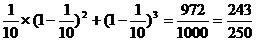
答:检测中不发生故障的次数大于发生故障的次数的概率为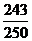 . ………………12分.
. ………………12分.
[点评]本小题主要考查相互独立事件,独立重复试验、互斥事件等概念及相关计算,考查运用概率知识与方法解决实际问题的能力.
18、(本小题满分12分) 已知函数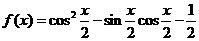 。
。
(Ⅰ)求函数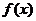 的最小正周期和值域;
的最小正周期和值域;
(Ⅱ)若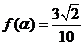 ,求
,求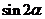 的值。
的值。
[解析](1)由已知,f(x)=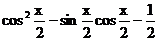
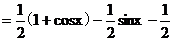
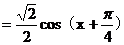
所以f(x)的最小正周期为2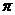 ,值域为
,值域为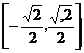 。…………………6分
。…………………6分
(2)由(1)知,f(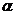 )=
)=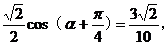
所以cos(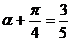 )。
)。
所以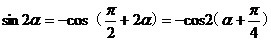
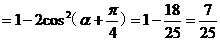 ,…………………12分
,…………………12分
[点评]本小题主要考查三角函数的性质、两角和的正(余)弦公式、二倍角公式等基础知识,考查运算能力,考查化归与转化等数学思想.
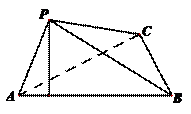
19、(本小题满分12分) 如图,在三棱锥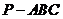 中,
中,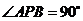 ,
,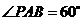 ,
,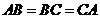 ,点
,点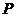 在平面
在平面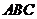 内的射影
内的射影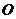 在
在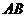 上。
上。
(Ⅰ)求直线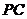 与平面
与平面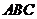 所成的角的大小;
所成的角的大小;
(Ⅱ)求二面角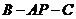 的大小。
的大小。
[解析](1)连接OC. 由已知,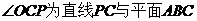 所成的角
所成的角
设AB的中点为D,连接PD、CD.
因为AB=BC=CA,所以CD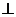 AB.
AB.
因为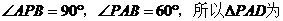 等边三角形,
等边三角形,
不妨设PA=2,则OD=1,OP=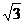 , AB=4.
, AB=4.
所以CD=2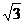 ,OC=
,OC=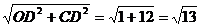 .
.
在Rt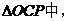 tan
tan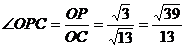 .…………………………6分
.…………………………6分
(2)过D作DE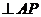 于E,连接CE.
于E,连接CE.
由已知可得,CD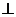 平面PAB.
平面PAB.
据三垂线定理可知,CE⊥PA,
所以,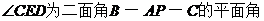 .
.
由(1)知,DE=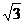
在Rt△CDE中,tan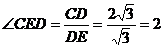
故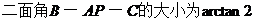 …………………………………12分
…………………………………12分
[点评]本题旨在考查线面位置关系和二面角的基础概念,重点考查思维能力和空间想象能力,进一步深化对二面角的平面角的求解.求解二面角平面角的常规步骤:一找(寻找现成的二面角的平面角)、二作(若没有找到现成的,需要引出辅助线作出二面角的平面角)、三求(有了二面角的平面角后,在三角形中求出该角相应的三角函数值).
20、(本小题满分12分) 已知数列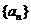 的前
的前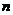 项和为
项和为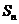 ,常数
,常数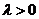 ,且
,且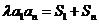 对一切正整数
对一切正整数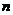 都成立。
都成立。
(Ⅰ)求数列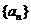 的通项公式;
的通项公式;
(Ⅱ)设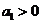 ,
,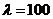 ,当
,当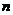 为何值时,数列
为何值时,数列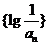 的前
的前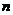 项和最大?
项和最大?
[解析]取n=1,得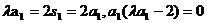
若a1=0,则s1=0, 当n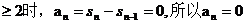
若a1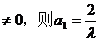 , 当n
, 当n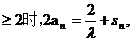
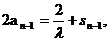
上述两个式子相减得:an=2an-1,所以数列{an}是等比数列
综上,若a1 = 0, 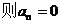
若a1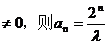 …………………………………………7分
…………………………………………7分
(2)当a1>0,且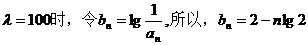
所以,{bn}单调递减的等差数列(公差为-lg2)
则 b1>b2>b3>…>b6=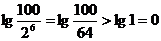
当n≥7时,bn≤b7=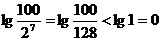
故数列{lg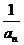 }的前6项的和最大. …………………………12分
}的前6项的和最大. …………………………12分
[点评]本小题主要从三个层面对考生进行了考查. 第一,知识层面:考查等差数列、等比数列、对数等基础知识;第二,能力层面:考查思维、运算、分析问题和解决问题的能力;第三,数学思想:考查方程、分类与整合、化归与转化等数学思想.
21、(本小题满分12分) 如图,动点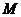 与两定点
与两定点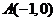 、
、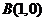 构成
构成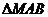 ,且直线
,且直线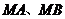 的斜率之积为4,设动点
的斜率之积为4,设动点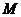 的轨迹为
的轨迹为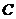 。
。
(Ⅰ)求轨迹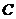 的方程;
的方程;
(Ⅱ)设直线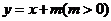 与
与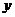 轴交于点
轴交于点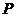 ,与轨迹
,与轨迹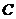 相交于点
相交于点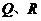 ,且
,且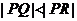 ,求
,求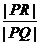 的取值范围。
的取值范围。
[解析](1)设M的坐标为(x,y),当x=-1时,直线MA的斜率不存在;当x=1时,直线MB的斜率不存在。
于是x≠1且x≠-1.此时,MA的斜率为
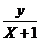 ,MB的斜率为
,MB的斜率为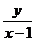 .
.
由题意,有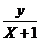 ·
·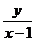 =4
=4
化简可得,4x2-y2-4=0
故动点M的轨迹C的方程为4x2-y2-4=0(x≠1且x≠-1)…………………………4分
(2)由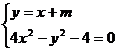 消去y,可得3x2-2mx-m2-4=0. (﹡)
消去y,可得3x2-2mx-m2-4=0. (﹡)
对于方程(﹡),其判别式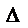 =(-2m)2-4×3(-m2-4)=16m2+48>0
=(-2m)2-4×3(-m2-4)=16m2+48>0
而当1或-1为方程(*)的根时,m的值为-1或1.
结合题设(m>0)可知,m>0,且m≠1
设Q、R的坐标分别为(XQ,YQ),(XR,YR),则为方程(*)的两根.
因为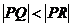 ,所以
,所以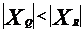 ,
,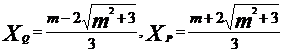
所以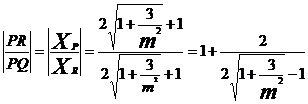 。
。
此时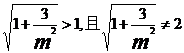
所以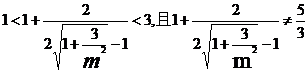
所以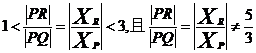
综上所述, …………………………12分
…………………………12分
[点评]本小题主要考察直线、双曲线、轨迹方程的求法等基础知识,考察思维能力、运算能力,考察函数、分类与整合等思想,并考察思维的严谨性。
22、(本小题满分14分) 已知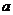 为正实数,
为正实数,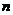 为自然数,抛物线
为自然数,抛物线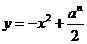 与
与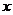 轴正半轴相交于点
轴正半轴相交于点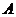 ,设
,设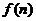 为该抛物线在点
为该抛物线在点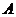 处的切线在
处的切线在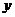 轴上的截距。
轴上的截距。
(Ⅰ)用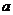 和
和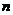 表示
表示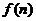 ;
;
(Ⅱ)求对所有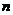 都有
都有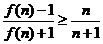 成立的
成立的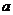 的最小值;
的最小值;
(Ⅲ)当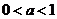 时,比较
时,比较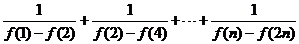 与
与
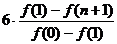 的大小,并说明理由。
的大小,并说明理由。
[解析](1)由已知得,交点A的坐标为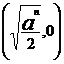 ,对
,对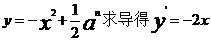
则抛物线在点A处的切线方程为:
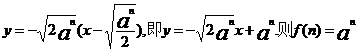 ………………4分
………………4分
(2)由(1)知f(n)=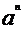 ,则
,则
即知,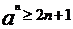 对于所有的n成立,
对于所有的n成立,
特别地,当n=1时,得到a≥3
当a=3,n≥1时,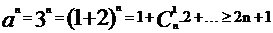
当n=0时,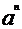 =2n+1.故a=3时
=2n+1.故a=3时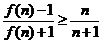 对所有自然数n均成立.
对所有自然数n均成立.
所以满足条件的a的最小值为3. ………………………………………………8分
(3)由(1)知f(k)=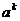
下面证明: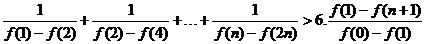
首先证明0<x<1时,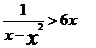
设函数g(x)=6x(x2-x)+1,0<x<1, 则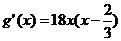 .
.
当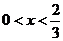 时,g'(x)<0; 当
时,g'(x)<0; 当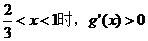
故g(x)在区间(0,1)上的最小值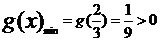
所以,当0<x<1时,g(x)>0,即得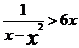
由0<a<1知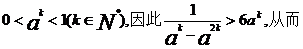
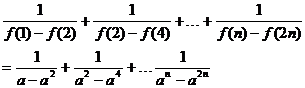
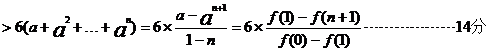
[点评]本小题属于高档题,难度较大,需要考生具备扎实的数学基础和解决数学问题的能力.主要考查了导数的应用、不等式、数列等基础知识;考查了思维能力、运算能力、分析问题与解决问题的能力和创新意识能力;且又深层次的考查了函数、转换与化归、特殊与一般等数学思维方法。












